This is the 12th installment of the 'Getting Started' series. Furthermore, this is the third of three posts about the three statements that you can use in PROC SGPLOT that fit regression functions: REG, PBSPLINE, and LOESS.

This is the 12th installment of the 'Getting Started' series.Furthermore, this is the third of three posts about the three statements that you can use in PROC SGPLOT that fit regression functions: REG, PBSPLINE, and LOESS. R/fitPlot.R defines the following functions: iFitPlotLtys2 iFitPlotPchs2 iFitPlotClrs2 iCIfp iCIfp1 fitPlot.logreg fitPlot.glm fitPlot.nls fitPlot.TWOWAY fitPlot.POLY iFitPlotIVR2 iFitPlotIVR1 fitPlot.IVR fitPlot.SLR fitPlot.lm.

FitPlot Alternatives. The most popular alternative is BookletCreator, which is free. If that doesn't suit you, our users have ranked 6 alternatives to FitPlot so hopefully you can find a suitable replacement. Other interesting FitPlot alternatives are Qimage Ultimate (Paid), Create Booklet (Paid), Cocoabooklet (Free Personal) and Cheap Impostor. /. Open the LISTING destination and assign the ANALYSIS style to the graph./ ods listing style=analysis; ods graphics / width=5in height=2.81in; title 'Mileage. Plot(cfit) plots the cfit object over the domain of the current axes, if any.If there are no current axes, and fun is an output from the fit function, the plot is over the domain of the fitted data.

Loess is a statistical methodology that performs locally weighted scatter plot smoothing. Loess provides the nonparametric method for estimating regression surfaces that was pioneered by William S. Cleveland and colleagues. The methodology behind the LOESS statement, like the PBSPLINE statement (and unlike the REG statement), makes no assumptions about the parametric form of the regression function. The LOESS statement provides some of the same methods that are available in PROC LOESS.

Fitflop Shoes

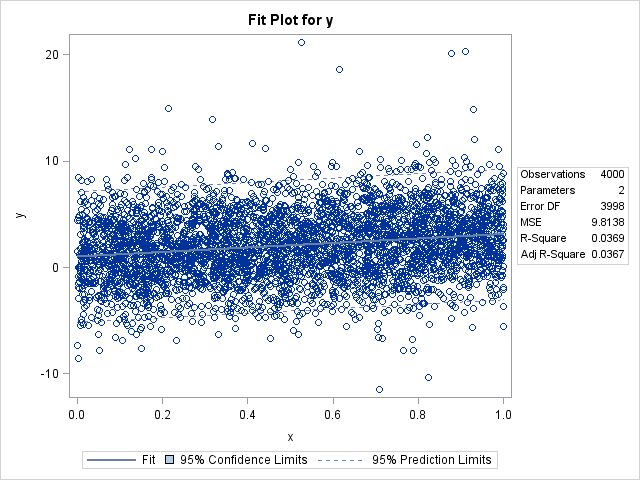
The LOESS statement fits loess models, displays the fit function(s), and optionally displays the data values. You can fit a wide variety of curves. You can fit a single function, or when you have a group or classification variable, fit multiple functions. (PROC SGPLOT provides a GROUP= option whereas statistical procedures usually provide a CLASS statement that you can use to specify groups.)

The following step displays a single curve and a scatter plot of points.

You can specify the GROUP= option in the LOESS statement to get a separate fit function for each group. You can also specify ATTRPRIORITY=NONE in the ODS GRAPHICS statement and a STYLEATTRS statement to vary the markers for each group while using solid lines.

The DEGREE= option specifies the degree of the local polynomials to use for each local regression. Specify either 1 (linear fit, the default) or 2 (quadratic fit). The results are often similar.

In many cases, the LOESS and PBSPLINE statements produce similar results.

If you want more control over the smoothing options, you can use PROC LOESS. The Sashelp.ENSO data set provides a particularly nice example since the smoothing parameter has both a local and a global optimum. The global optimum shows the effect of seasons, whereas the local optimum shows the effect of El Nino. By default, PROC LOESS finds the local optimum for this data set.

There are many ways you can force it to find the global optimum. This next example specifies a generalized cross-validation criterion and the range for the smoothing parameter.

Then you can specify the smoothing parameter in a LOESS statement in PROC SGPLOT. The LOESS statement in PROC SGPLOT uses different default options than PROC LOESS, so this example forces PROC SGPLOT's LOESS statement to find the local optimum, which is displayed along with the global optimum.

You can additionally specify INTERPOLATION=LINEAR or INTERPOLATION=CUBIC to control the degree of the interpolating polynomials (not shown here).

Linear modeling procedures, such as PROC REG, use loess to find trends in residuals. These trends can help you identify lack of fit and build better models.

References

Cleveland,W. S., Devlin, S. J., and Grosse, E. (1988). 'Regression by Local Fitting.' Journal of Econometrics 37:87-114.

Cleveland, W. S., and Grosse, E. (1991). 'Computational Methods for Local Regression.' Statistics and Computing 1:47-62.

Cleveland, W. S., Grosse, E., and Shyu, M.-J. (1992). 'A Package of C and Fortran Routines for Fitting Local Regression Models.' Unpublished manuscript.

Continuing the discussion on cumulative odds models I started last time, I want to investigate a solution I always assumed would help mitigate a failure to meet the proportional odds assumption. I’ve believed if there is a large number of categories and the relative cumulative odds between two groups don’t appear proportional across all categorical levels, then a reasonable approach is to reduce the number of categories. In other words, fewer categories translates to proportional odds. I’m not sure what led me to this conclusion, but in this post I’ve created some simulations that seem to throw cold water on that idea.

When the odds are proportional

I think it is illustrative to go through a base case where the odds are actually proportional. This will allow me to introduce the data generation and visualization that I’m using to explore this issue. I am showing a lot of code here, because I think it is useful to see how it is possible to visualize cumulative odds data and the model estimates.

The first function genDT generates a data set with two treatment arms and an ordinal outcome. genOrdCat uses a base set of probabilities for the control arm, and the experimental arm probabilities are generated under an assumption of proportional cumulative odds (see the previous post for more details on what cumulative odds are and what the model is).

In this case, I’ve set the base probabilities for an ordinal outcome of 8 categories. The log of the cumulative odds ratio comparing experimental arm to control is 1.0 (and is parameterized as -1.0). In this case, the proportional odds ratio should be about 2.7.

Clear memory cache windows 7. Calculation of the observed cumulative odds ratio at each response level doesn’t provide an entirely clear picture about proportionality, but the sample size is relatively small given the number of categories.

A visual assessment

An excellent way to assess proportionality is to do a visual comparison of the observed cumulative probabilities with the estimated cumulative probabilities from the cumulative odds model that makes the assumption of proportional odds.

I’ve written three functions that help facilitate this comparison. getCumProbs converts the parameter estimates of cumulative odds from the model to estimates of cumulative probabilities.

The function bootCumProb provides a single bootstrap from the data so that we can visualize the uncertainty of the estimated cumulative probabilities. In this procedure, a random sample is drawn (with replacement) from the data set, a clm model is fit, and the cumulative odds are converted to cumulative probabilities.

The third function fitPlot fits a clm model to the original data set, collects the bootstrapped estimates, calculates the observed cumulative probabilities, converts the estimated odds to estimated probabilities, and generates a plot of the observed data, the model fit, and the bootstrap estimates.

Here is a plot based on the original data set of 200 observations. The observed values are quite close to the modeled estimates, and well within the range of the bootstrap estimates.

Collapsing the categories

Continuing with the same data set, let’s see what happens when we collapse categories together. I’ve written a function collapseCat that takes a list of vectors of categories that are to be combined and returns a new, modified data set.

Here is the distribution of the original data set:

And if we combine categories 1, 2, and 3 together, as well as 7 and 8, here is the resulting distribution based on the remaining five categories. Here’s a quick check to see that the categories were properly combined:

Hsds usb devices driver. If we create four modified data sets based on different combinations of groups, we can fit models and plot the cumulative probabilities for all for of them. In all cases the proportional odds assumption still seems pretty reasonable.

Non-proportional cumulative odds

That was all just a set-up to explore what happens in the case of non-proportional odds. To do that, there’s just one more function to add - we need to generate data that does not assume proportional cumulative odds. I use the rdirichlet in the gtools package to generate values between 0 and 1, which sum to 1. The key here is that there is no pattern in the data - so that the ratio of the cumulative odds will not be constant.

Fitplates

Again, we generate a data set with 200 observations and an ordinal categorical outcome with 8 levels. The plot of the observed and estimated cumulative probabilities suggests that the proportional odds assumption is not a good one here. Some of the observed probabilities are quite far from the fitted lines, particularly at the low end of the ordinal scale. It may not be a disaster to to use a clm model here, but it is probably not a great idea.

Fitplot

The question remains - if we reduce the number of categories does the assumption of proportional odds come into focus? The four scenarios shown here do not suggest much improvement. The observed data still fall outside or at the edge of the bootstrap bands for some levels in each case.

Fit Plot Mathematica

What should we do in this case? That is a tough question. The proportional odds model for the original data set with eight categories is probably just as reasonable as estimating a model using any of the combined data sets; there is no reason to think that any one of the alternatives with fewer categories will be an improvement. And, as we learned last time, we may actually lose power by collapsing some of the categories. So, it is probably best to analyze the data set using its original structure, and find the best model for that data set. Ultimately, that best model may need to relax the proportionality assumption; a post on that will need to be written another time.